Dijkstra算法 | 一人Code

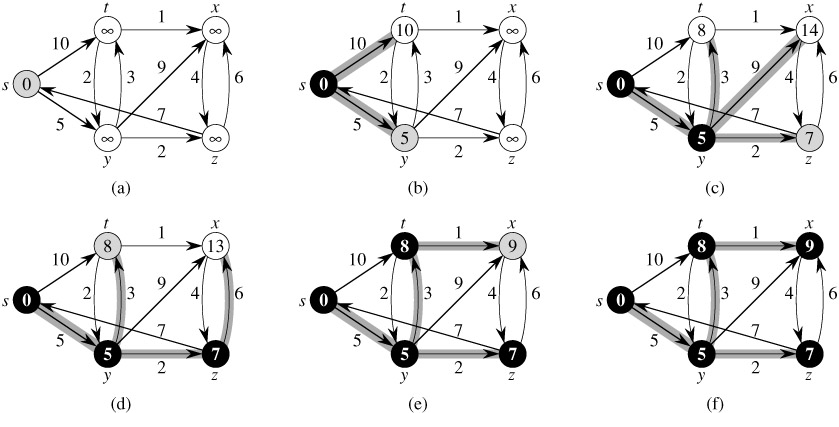
介绍

Dijkstra算法(Dijkstra’s algorithm)是解决单源最短路径问题的一般算法。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

算法思想

在每个阶段，Dijkstra算法选择一个顶点v,它在所有未知顶点中具有最小的dv，同时声明从s到v的最短路径是已知的。阶段的其余部分由dw值的更新工作组成。

这里先明确两个集合：所有顶点集V和已选中顶点集S。

• 找到当前未选中点（V - S）中距离源点最近的点

• 更新未选中点到源点的距离

核心代码

我觉得<<数据结构与算法分析–C语言描述>>中的伪代码言简意赅，我将在Github中放上具体实现，此处就放上书上源码。

Dijkstra算法的声明

typedef int Vertex;

struct TableEntery
{
	List Header;	// Adjacency list
	int Known;
	DisType Dist;
	Vertex Path;
};

// Vertices are numbered from 0
# define NotAVertex (-1)
typedef struct TableEntery Table[NumVertex];

表初始化

void InitTable(Vertex Start, Graph G, Table T)
{
	int i;

	ReadGrap(G, T);	// Read graph somehow
	for(i = 0; i < NumVertex; i++)
	{
		T[i].Known = False;
		T[i].Dist = Infinity;
		T[i].Path = NotAVertex;
	}
	T[Start].Dist = 0;
}

显示实际最短路径

// print shorting path to V after Dijkstra has run
// Assume that the path exists

void PrintPath(Vertex V, Table T)
{
	if(T[V].Path != NotAVertex)
	{
		PrintPath(T[V].Path, T);
		printf(" to ");
	}
	printf("%v", V);	// %v is pseudocode
}

Dijkstra算法的伪代码

void Dijkstra(Table T)
{
	Vertex V, W;
	for(;;)
	{
		V = smallest unknown distance vertex;
		if(V == NotAVertex)
			break;

		T[V].Known = True;
		for each W adjacent to V
			if(!T[W].Known)
				if(T[V].Dist + Cvw < T[W].Dist)
				{		// Update W
					Decrease(T[W].Dist to T[V].Dist + Cvw);
					T[W].Path =  V;
				}
	}
}

总结

Dijkstra算法适用于图的边没有负值。时间复杂度也要看具体实现。

我个人认为，算法思路很容易理解，在代码的实现细节上可能存在一些难点。